Math

📜 Description 题面

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.

给出两个非空的链表用来表示两个非负的整数。其中，它们各自的位数是按照逆序的方式存储的，并且它们的每个节点只能存储一位数字。

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

Input: (2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 0 -> 8
Explanation: 342 + 465 = 807.

🔗 Link 链接

LeetCode: https://leetcode.com/problems/add-two-numbers/

力扣：https://leetcode-cn.com/problems/add-two-numbers/

❓ Solution 题解

Approach: Elementary Math 初等数学

Intuition 思路

Keep track of the carry using a variable and simulate digits-by-digits sum starting from the head of list, which contains the least-significant digit.

我们使用变量来跟踪进位，并从包含最低有效位的表头开始模拟逐位相加的过程。

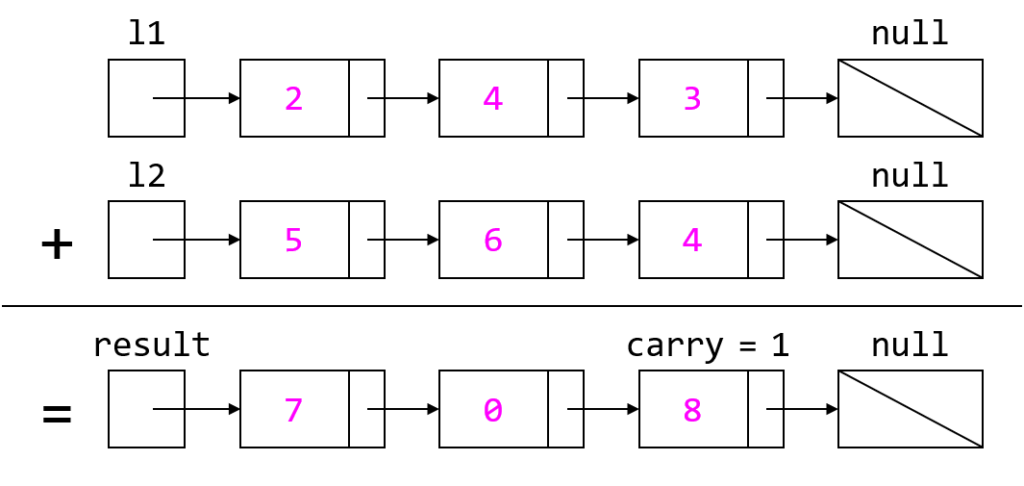
Figure 1. Visualization of the addition of two numbers: $342 + 465 = 807$ .
Each node contains a single digit and the digits are stored in reverse order.
图1，对两数相加方法的可视化： $342 + 465 = 807$ 。
每个结点都包含一个数字，并且数字按位逆序存储。

Algorithm 算法

Just like how you would sum two numbers on a piece of paper, we begin by summing the least-significant digits, which is the head of $l1$ and $l2$ . Since each digit is in the range of $0...9$ , summing two digits may “overflow”. For example $5 + 7 = 12$ . In this case, we set the current digit to $2$ and bring over the $carry = 1$ to the next iteration. $carry$ must be either $0$ or $1$ because the largest possible sum of two digits (including the carry) is $9 + 9 + 1 = 19$ .

就像你在纸上计算两个数字的和那样，我们首先从最低有效位也就是列表 $l1$ 和 $l2$ 的表头开始相加。由于每位数字都应当处于 $0...9$ 的范围内，我们计算两个数字的和时可能会出现 “溢出”。例如， $5 + 7 = 12$ 。在这种情况下，我们会将当前位的数值设置为 $2$ ，并将进位 $carry = 1$ 带入下一次迭代。进位 $carry$ 必定是 $0$ 或 $1$ ，这是因为两个数字相加（考虑到进位）可能出现的最大和为 $9 + 9 + 1 = 19$ 。

The pseudocode is as following:

伪代码如下：

Initialize current node to dummy head of the returning list.
Initialize $carry$ to $0$ .
Initialize $p$ and $q$ to head of $l1$ and $l2$ respectively.
Loop through lists l1 and l2 until you reach both ends.
- Set $x$ to node $p$ ‘s value. If $p$ has reached the end of $l1$ , set to $0$ .
- Set $y$ to node $q$ ‘s value. If $q$ has reached the end of $l2$ , set to $0$ .
- Set $sum = x + y + carry$ .
- Update $carry = sum / 10$ .
- Create a new node with the digit value of $(sum \bmod 10)$ and set it to current node’s next, then advance current node to next.
- Advance both $p$ and $q$ .
Check if $carry = 1$ , if so append a new node with digit $1$ to the returning list.
Return dummy head’s next node.

将当前结点初始化为返回列表的哑结点。
将进位 $carry$ 初始化为 $0$ 。
将 $p$ 和 $q$ 分别初始化为列表 $l1$ 和 $l2$ 的头部。
遍历列表 l1 和 l2 直至到达它们的尾端。
- 将 $x$ 设为结点 $p$ 的值。如果 $p$ 已经到达 $l1$ 的末尾，则将其值设置为 $0$ 。
- 将 $y$ 设为结点 $q$ 的值。如果 $q$ 已经到达 $l2$ 的末尾，则将其值设置为 $0$ 。
- 设定 $sum = x + y + carry$ 。
- 更新进位的值， $carry = sum / 10$ 。
- 创建一个数值为 $(sum \bmod 10)$ 的新结点，并将其设置为当前结点的下一个结点，然后将当前结点前进到下一个结点。
- 同时，将 $p$ 和 $q$ 前进到下一个结点。
检查 $carry = 1$ 是否成立，如果成立，则向返回列表追加一个含有数字 $1$ 的新结点。
返回哑结点的下一个结点。

Note that we use a dummy head to simplify the code. Without a dummy head, you would have to write extra conditional statements to initialize the head’s value.

请注意，我们使用哑结点来简化代码。如果没有哑结点，则必须编写额外的条件语句来初始化表头的值。

Take extra caution of the following cases:

请特别注意以下情况：

Test case 测试用例	Explanation 说明
$l1=[0,1]$ $l2=[0,1,2]$	When one list is longer than the other. 当一个列表比另一个列表长时。
$l1=[]$ $l2=[0,1]$	When one list is null, which means an empty list. 当一个列表为空时，即出现空列表。
$l1=[9,9]$ $l2=[1]$	The sum could have an extra carry of one at the end, which is easy to forget. 求和运算最后可能出现额外的进位，这一点很容易被遗忘。

Complexity Analysis 复杂度分析

Time complexity : $O(\max(m, n))$ . Assume that $m$ and $n$ represents the length of $l1$ and $l2$ respectively, the algorithm above iterates at most $\max(m, n)$ times.
Space complexity : $O(\max(m, n))$ . The length of the new list is at most $\max(m, n)+1$ .

时间复杂度： $O(\max(m, n))$ ，假设 $m$ 和 $n$ 分别表示 $l1$ 和 $l2$ 的长度，上面的算法最多重复 $\max(m, n)$ 次。
空间复杂度： $O(\max(m, n))$ ，新列表的长度最多为 $\max(m, n)+1$ 。

Follow up 拓展

What if the the digits in the linked list are stored in non-reversed order? For example:

如果链表中的数字不是按逆序存储的呢？例如：

$(3 \to 4 \to 2) + (4 \to 6 \to 5) = 8 \to 0 \to 7$

📝 Code 代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
	ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
		int iCarry = 0;
		ListNode* pBegin = new ListNode(0);
		ListNode* pEnd = pBegin;

		while (l1 || l2 || iCarry) {
			int iSum = (l1 ? l1->val : 0) + (l2 ? l2->val : 0) + iCarry;
			iCarry = iSum / 10;
			pEnd->next = new ListNode(iSum % 10);
			pEnd = pEnd->next;
			l1 = l1 ? l1->next : l1;
			l2 = l2 ? l2->next : l2;
		}

		ListNode* pAns = pBegin->next;
		delete pBegin;
		return pAns;
	}
};